Recursion simply means the process of repeating items in a self-similar way. The recursion function in python or any other programming language allows you to call a function inside the same function.

When we consider repeating a task, we normally consider the for and while loops. These constructs allow us to iterate through a list, collection, or different facts structure.

However, there may be some other manner to repeat work in a slightly different manner. Recursion is executed by invoking a characteristic internal itself to solve a smaller example of the equal issue.

These functions call themselves until the issue is addressed, thereby breaking the original issue into many smaller instances of itself – similar to eating little nibbles of a bigger piece of food.

The ultimate aim is to consume the whole plate of hot pockets by repeatedly taking bites. Each chunk is a recursive action, because of this that you repeat the method of the following time.

You do this for each mouthful, deciding whether or not to eat another to fulfill your objective until there are no hot pockets left on your plate.

What is the Recursion function in Python?

As indicated withinside the introduction, recursion includes a mechanism withinside the definition invoking itself. A recursive function typically consists of two parts:

• The base case is a condition that indicates when the recursive function should be terminated.
• The call to action

Definition of Recursion

“Recursion refers to a method of programming or coding a problem, in this method, a function calls itself one or more times in its body. And it is returning the return value of this function call. Be it in any programming language, if a function satisfies the condition of recursion, we call this function a recursive function.”

Let’s look at a simple example to show both components:

# Assume that remaining is a positive integer
def hi_recrusive (remaining):
    # The base case
    if remaining == 0:
        return
    print (‘hi’)

    #call to function, with a reduced remaining count
    hi_recursive (remaining - 1)

For us, the basic case is whether the remaining variable is equal to zero, indicating how many more “hi” strings we must display. The function just returns.

Following the print statement, we name hi_recursive as soon as again, however with a decrease ultimate cost.

This is critical! If the cost of ultimate isn’t always decreased, the feature will execute forever. When a recursive feature calls itself, the arguments are frequently altered to be towards the bottom case.

Let’s see what happens when we call hi_recursive(3):

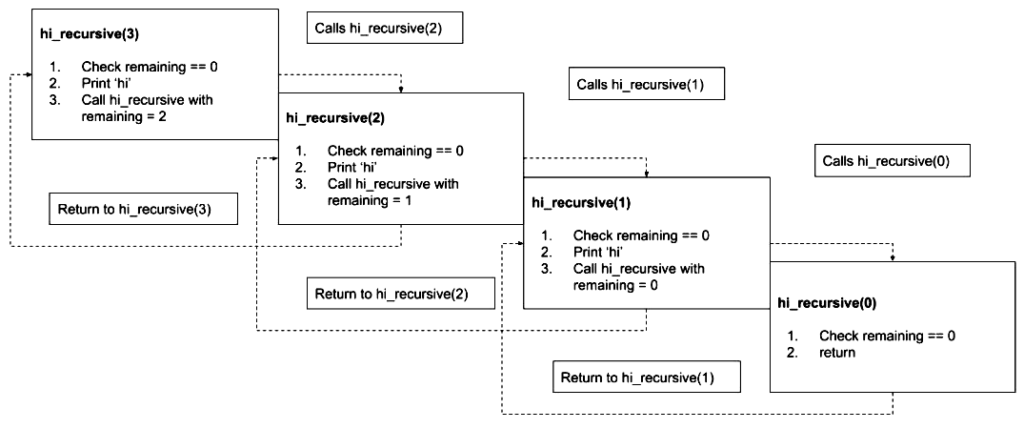
After printing ‘hello,’ the function calls itself with a smaller value for remaining until it approaches 0.

At zero, the function returns to the point where it was called in hi_recursive(1), which in turn returns to the point where it was called in hi_recursive(2), which eventually returns to the point where it was called in hi_recursive(1) (3).

Why not use a Loop?

Loops may be used to manage any traversal. Even said, recursion is frequently more effective than iteration in solving certain problems. Tree traversal is a popular use for recursion:

When utilizing recursion, traversing through the nodes and leaves of a tree is typically simpler to conceive about.

Although both loops and recursion traverse the tree, they serve distinct purposes: loops are used to repeat a job, while recursion is used to divide a big work into smaller jobs.

For example, recursion works nicely with trees due to the fact we will method the entire tree by processing smaller sections of the tree separately.

Illustrations

The best approach to get acquainted with recursion, or any other programming topic, is to put it into practice.

Creating recursive features is simple: include your base case and contact the characteristic such that it comes toward the bottom case.

Recursion Function in Python described as follows;

A List’s Sum

def sum_recursive (nums) :
    if len (num) == 0:
        return 0

    last_num = nums . pop ()
    return last_num + sum_recursive (nums)

Python has a list sum function.

To produce such functions, the default Python implementation, C, Python, uses an endless for-loop in C. (source code right here for the ones interested).

Let’s have a look at how to achieve it using recursion:

The simplest situation is an empty list, for which the best sum is 0. Now that we’ve dealt with our base case, let’s remove the last item from the list.

Finally, we’ll use the smallest list to perform the sum_recursive addition function and add the number we’ve extracted to the grand total.

Sum([10, 5, 2]) and sum_recursive([10, 5, 2]) in a Python interpreter should both return 17.

Numbers in Factorial Form

You can remember that the factorial of a positive integer is the product of all of the above numbers. The following example helps to clarify:

5! = 5 x 4 x 3 x 2 x 1 = 120

The exclamation symbol indicates a factorial, and we can see that we multiply 5 by the product of all numbers from 4 to 1. What happens if someone enters 0? It is universally accepted and shown that

0! = 1. Now, let’s write the following function:

def factorial (n):
    if n == 0 or n == 1:
       return 1
    return n “ factorial (n - 1)

We account for scenarios when 1 or 0 are inputted, and otherwise, we multiply the current number by the factorial of the number reduced by 1.

Now Let’s see the Advantages and disadvantages or limitations of writing code with the recursion function in python or any other language.

Advantages of Recursion function

• It makes the code look clean and easy to read.
• A complex code can be broken down into simple sub-problems.
• it is useful in making repetitive type solutions to a problem.
• it is used with the data structures such as stack, queues, linked-List, etc.

Disadvantages of Recursion function

• The recursion function uses more memory space.
• Recursive algorithms have more overhead and can cause a stack overflow.
• the program can fail if the depth of recursion is too large.
• Methods call in recursion may be time-consuming.
• Recursion functions are expensive and inefficient as they consume a lot of memory.

Conclusion:

Recursion enables us to divide a complex job into smaller jobs by continually invoking itself.

A recursive function needs a base case to stop execution and a call to itself that gradually brings the function into the base case.

It’s most typically utilized in trees, but recursion may also be utilized in other functions to give attractive solutions.

Nowadays, almost all computer programming languages support recursion by allowing a function to call itself from within its own code.

When and Where to Use Recursion function?

Here are the simple bullet points regarding when to use the recursion function and when to avoid using it.

Use Recursion function only if:

• the problem definition is recursive,
• the problem is simple to solve recursively,
• the produced results are used in the reverse order of their creations.

Don’t use the Recursion function If,

• the recursion can be replaced with only a loop.
• there is a run time or space limitation.