Hamming codes are a family of linear error-correcting codes and it is named after Richard W Hamming. In this article, we have shared the history of Hamming code and its uses in computer science, and code error detection calculations with examples.
What is Hamming Code?
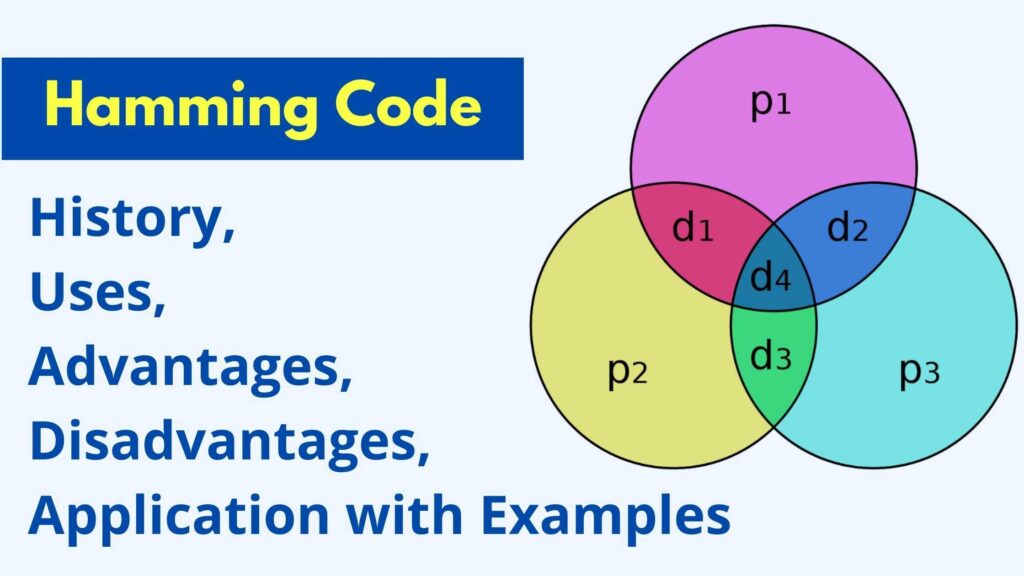
Hamming code is a type of liner code that can detect up to two instantaneous bit mistakes. Single-bit mistakes are possible.
The source encodes the message in Hamming code by adding superfluous bits to the message. The majority of these redundant bits are added and created at specific points in the message to aid in the mistake identification and correction process.
History of Hamming Code:
The Hamming code has a long history. The Hamming Code technique was developed by American Mathematician Richard W. Hamming to detect errors and correcting them.
Mr. Richard published a paper in 1950 in which he introduced a concept of the number of positions in which two code-words differ and the number of changes required to transform one code-word into another. It is now popularly known as Hamming distance.
After this study, Hamming created a family of mathematical error-correcting codes, which today we called Hamming codes.
This landmark study not only solved an important problem in telecommunications and computer science, but it introduced a whole new field of study.
He created the Hamming Code which is still commonly used today in applications such as ECC memory. ECC stands for Error correction-code memory.
Hamming code, which leverages the relationship between data and redundancy bits, should be applied to data units of any length.
He worked on the problem of error correction and developed the Hamming code, a set of increasingly powerful algorithms. Hamming code is used in a variety of fields.
Uses of Hamming Code
Here are a few examples of how Hamming code is used in the industries.
- Used in Satellites
- Used in Computer Memory
- Used in Modems
- Used in PlasmaCAM
- Used in Open connectors
- Used in Shielding wire
- Used in Embedded Processor
Advantages of Hamming Code
Hamming code has many benefits. They are used for various purposes in many applications…
- On networks where data streams are delivered for single-bit mistakes, the Hamming coding approach is effective.
- Hamming code not only detects bit errors but also aids in the identification of bits containing errors so that they can be repaired.
- Because of their simplicity, hamming codes are ideal for computer memory and single-error correction.
Disadvantages of Hamming Code
For everything, there will be advantages and disadvantages. so, hamming code has disadvantages along with advantages
- Error detection and correction code for single bits. If numerous bits are determined to be incorrect, the result may be that another bit that should be accurate is modified. This may lead the data to become even more erroneous.
- The Hamming coding algorithm can only address single-bit problems.
- Hamming Code is a method of encoding a message.
Must Read ➜ Recursion Function in Python
Example of Hamming Code:
Here’s an example of hamming code. We can detect errors by using this.
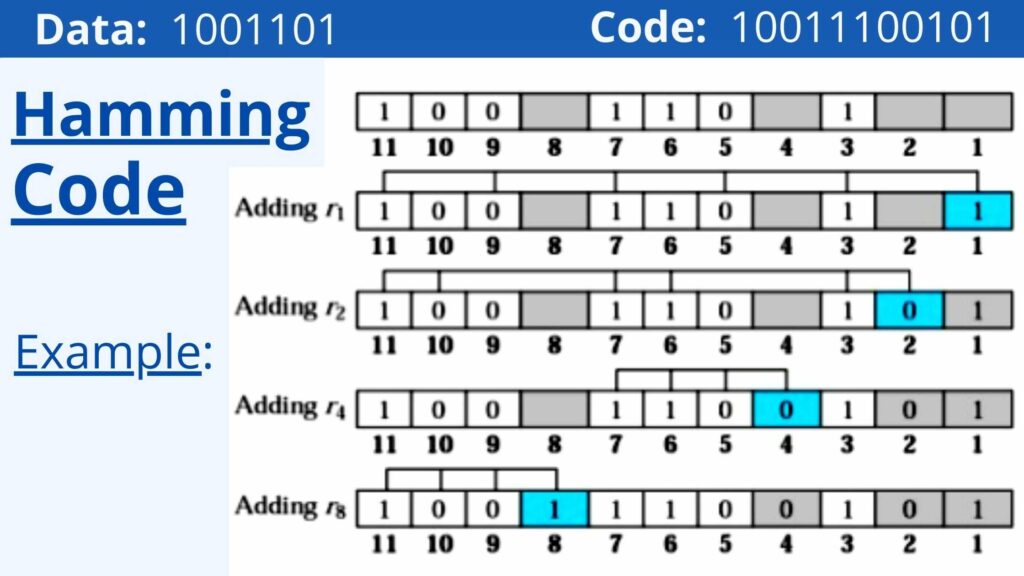
Applications of Hamming-Code
Application of Hamming codes can be understood by using it in encoding and decrypting a message.
Process of Encoding & Decrypting a Message
The sender’s technique for encoding the message includes the following three steps:
- The total number of superfluous bits is calculated.
- Examining the superfluous bits’ locations.
- Finally, the values of these superfluous bits must be calculated.
The message is sent to the user after the above superfluous bits have been inserted into it. Follow the below steps and try to understand.
Step 1: Determine how many redundant bits there are in total.
Assume the message has the following information:
“n” is the number of bits in a data set.
p – the number of superfluous bits inserted so that np can represent at least (n + p + 1) different states.
In this case, (n + p) represents the location of an error in each of the (n + p) bit places, with one extra state indicating that there is no error.
Because p bits can represent 2p states, 2p must be at least (n+p+1).
Step 2: Repositioning the unnecessary components in their proper places.
The p superfluous bits should be inserted in powers of 2-bit places.
For instance, 1, 2, 4, 8, 16, and so on.
They are labeled as p1 (first position), p2 (second position), p3 (fourth position), and so on.
Step 3: Calculation of the unnecessary bit’s values.
The redundant bits should be parity bits, resulting in an even or odd number of 1s.
What are the two sorts of parity?
- Even parity refers to the process of making the total number of bits in a message even.
- Odd parity refers to the process of making the total number of bits in a message odd.
All redundant bits, p1, must be calculated as parity in this case.
It should include all bit positions whose binary representation includes a 1 in the first place, with the exception of p1.
- P1 is the parity bit for all data bits in positions where the binary representation includes a 1 in the less important position, such as (3, 5, 7, 9,….).
- P2 is the parity bit for all data bits in binary representations that include 1 in position 2 from the right, but not 2 (3, 6, 7, 10, 11,…)
- P3 is the parity bit for every bit in a binary representation that includes a 1 in position 3 from the right, but not 4 (5-7, 12-15,… ).
In Hamming code, the process of decrypting a message is called Receiver receives incoming messages that necessitate recalculations to identify and repair problems.
The following are the steps in the recalculation process:
- Counting how many unnecessary bits there are.
- All superfluous bits are correctly positioned.
- Check for parity
- Counting the number of superfluous bits
Step 1: The number of superfluous bits can be calculated using the same formula.
n + p + 1 = 2p
The number of data bits is given, and the number of superfluous bits is given.
Step 2: Properly locating all unnecessary components p is a redundant bit that appears at bit positions with powers of 2, such as 1, 2, 4, 8, and so on.
Step 3: Perform a parity check
Data bits and redundant bits must be used to determine parity bits.
parity(1, 3, 5, 7, 9, 11...) p1 = parity(1, 3, 5, 7, 9, 11...) parity(2, 3, 6, 7, 10, 11... ) = p2 parity(4-7, 12-15, 20-23... ) = parity(4-7, 12-15, 20-23... ) = parity(4-7, 12-15, 20-23... )
Must Read ➜ Data Link Layer
Summary
Hamming code is a type of liner code that can detect up to two instantaneous bit mistakes. Single-bit mistakes are possible.
- R.W.Hamming developed the Hamming coding technique to detect faults.
- Satellites, Computer Memory, Modems, Embedded Processors, and other applications of Hemming code are common.
- This method of programming has a major advantage in that it works on networks where data streams are delivered for single-bit mistakes.
- The major flaw of this technique is that it can only address single-bit problems.
- With the use of hamming code, we can encrypt and decode the message.





